QCDLAT is a dedicated initiative within the field of theoretical physics of the INFN. Its main goal is to study the theory of strong interactions between quarks and gluons (Quantum ChromoDynamics, QCD) in order to understand the low-energy physical properties of hadrons, particles composed of quarks. In this low-energy regime, the coupling constant of the theory is large, making it necessary to use a discrete space-time lattice (LATtice) as a non-perturbative, first-principles computational method. Results in the continuum space-time are obtained through Monte Carlo numerical simulations on increasingly larger lattices with progressively finer lattice spacing. Non-perturbative lattice QCD calculations are crucial for achieving ever more precise theoretical predictions of hadronic observables. In the future, the comparison between theoretical results and experimental data may reveal the long-awaited signs of new physics beyond the Standard Model of elementary particle physics.
QCDLAT’s research activity focuses in particular on non-perturbative renormalization methods, which are essential for handling divergences in a quantum field theory. The renormalization scheme used by the group was developed within the framework of the international ALPHA collaboration and is based on recursive finite-volume techniques and specific boundary conditions for the fields in the functional integral. This approach enables the computation of the running of parameters over a wide range of energy scales, approximately ∼[4–100] GeV.
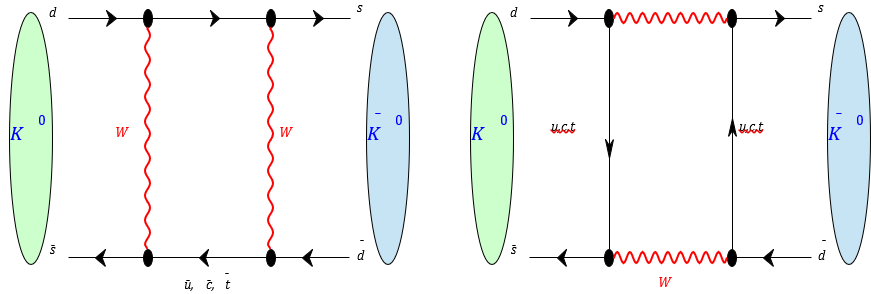
K¯0 antimeson due to weak interactions.
The group also studies neutral kaon oscillations. In the Standard Model, K0−K¯0 oscillations arise from quark flavor mixing governed by the Cabibbo-Kobayashi-Maskawa (CKM) matrix in weak interactions. In the effective description of the weak Hamiltonian, the operators responsible for neutral kaon oscillations are composed of four quark fields. In the Standard Model, there is only one effective four-fermion operator. However, in theories beyond the Standard Model (BSM), such as supersymmetry or multi-Higgs models, new operators can arise, including those with different chiral structures. In light of potential future signals of new physics, it is important to consider the full basis of all four-fermion operators with flavor change ∆F = 2.
Strong interactions between quarks involve gluon exchange and quark and gluon loops. Non-perturbative QCD corrections account for all possible exchanges at every order in the strong coupling constant.
References
Giulia Maria de Divitiis
Mauro Papinutto
Anastassios Vladikas
Publications
























































































